
Inequalities are a mathematical concept that is covered under the umbrella of algebra. If you don't remember these from school and want to know more about them, look no further. It's time for a little refresher.
In this article, we'll cover everything you need to know to write an inequality from a number line or a word problem.
We go into a lot of depth in this article. If you're already familiar with the basics of inequalities, feel free to skip straight to the section Write an Inequality from a Number Line or Write an Inequality from a Word Problem.
When it comes to writing an inequality, there are a few things that are useful to know. Let's dive into that information now.
Before we dive in, we’ll go over the basics you need to know to set you up for success when writing inequalities. Let’s start with a few definitions.
An 'inequality' is a mathematical concept found in algebra that enables you to compare the relationship between a given value and a variable.
Don’t worry if you’re not sure what that means. We’ll get on to the meaning of those words shortly.
Inequality comes in the form of an equation. It would look something like this:
x ≤ 20.
A variable represents a number that as of yet is unknown to us. It is usually labeled with a letter of the alphabet. The default letter that is used is ‘x’, but you could use any letter, such as, for example, the first letter of the word for which we don’t know the value.
Say we are looking to find out how many chocolates are left in the box, the variable here is the number of chocolates, so we could use the letter ‘c’ to refer to the unknown number.
A value is a number that we do know. It’s the one constant in the problem that’ll help us figure out the variable’s worth.
To use the above example of the chocolate box, if we know that the box, unopened, had 20 chocolates in it, then the number of chocolates left in the box can’t be more than 20. It is, therefore, less than or equal to 20.
The inequality equation might look a little something like this:
c ≤ 20
A number line is a visual representation of an inequality. The line can be used to place numbers on and along it, to show how different values and variables compare with one another.
The great thing about number lines is that they are infinite, meaning you can extend them as far as you want, and they can cover any imaginable range of numbers.
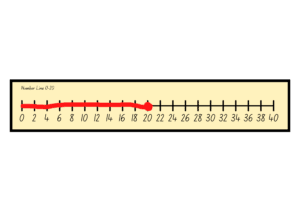
Let’s continue with the chocolate example. We know that the amount of chocolates left in the box is any number between 0 and 20. It can’t be more than 20, because the box when it was originally purchased, had 20 chocolates in it. So that’s the maximum amount. It also can’t be less than 0, because you can’t have a negative number of chocolates in a box.
The below number line represents the possible amount of chocolates left in the box: between 0 and 20.
If you think you don’t know what word problems are, we challenge you to think back to your school days and we’re certain that you’ll recall being regularly presented with mathematical problems to solve. They go something like this:
Sally had three pens at the beginning of the school day, but then her friend Josh gifted her one at lunchtime. Just a couple of hours later, Harry gifted her two pens. How many pens did Sally have at the end of the day?
Granted, this is a pretty basic additions problem, suited to a first-grade student, but you get the picture.
So before you can write an inequality, there are a few symbols you need to know about, as you’ll use them when you write an inequality.
The symbol ‘less than’ looks like this: < and means that the variable will be less than the value given.
For example, if we were to imagine that we had eaten one chocolate from the box, then we know that the number of chocolates left in the box could not be 30. It would have to be less than 30 since we know that at least one chocolate has been eaten. Therefore we would no longer be able to use the ‘less than or equal to’ symbol, so we would need to use the ‘less than’ symbol.
Using the ‘less than’ symbol, you would write this as such:
c < 30
The ‘more than’ symbol looks like such: > and means that the variable is going to be more than the given value.
To switch it up a little, let’s use the pen example from earlier. Sally had three pens at the beginning of the school day, but we know that she got given pens throughout the day. So we know for sure that by the end of the day she had more than 3 pens. Therefore, the equation would like a little something like this (using ‘p’ for ‘pens’):
p > 3
This means that the amount of pens that Sally has is more than 3. You could also say ‘greater than’.
This final kind of symbol is used to show that while we know that a variable is greater than or less than a value, we acknowledge that it could also be equal to that number.
To go back to our very first example, if we know the box of chocolates has been placed on the kitchen counter but we don’t know if anyone has eaten a chocolate from it yet, then what do we know? We know that there are no more than 30 chocolates in the box, that there could be less, and there could also be exactly 30, in the instance where nobody has opened the box yet.
We already covered what this equation would look like, but here it is again:
c ≤ 20
What about if the chocolates were for a party, and we knew that others might have also brought along a box of chocolates, but we didn’t know exactly how many people had? If we wanted to write an inequality about the number of boxes of chocolates present at the party, we would write (using bc to represent ‘boxes of chocolates’):
bc ≥ 1
That’s because we know there is at least one box of chocolates. There might be more, but we aren’t sure. Therefore, the amount of boxes of chocolates at the party is more than or equal to 1.
Now that we know what an inequality is, and we know what a word problem is, let’s dive into the topic at hand: how to write an inequality, first from a number line, and later from a word problem.
Let’s consider the following number line:
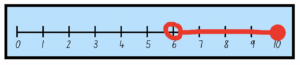
So first of all, you might notice that the red circle on the number 6 isn’t filled out, whereas the circle above the number 10 is colored in. This has a meaning.
If the circle is filled out, or ‘closed’, it means that the number is included. If it isn’t filled out, or ‘open’, this means that the number isn’t included.
So in this case, the variable does not include the number 6. It is greater than, but not equal to 6.
Let’s call the variable ‘x’. Here are the possible inequality equations for this number line:
x > 6
x ≤ 10
Or in other words, the variable ‘x’ is greater than 6 and less than or equal to 10.
You could also write it the following way:
10 ≥ x > 6
Indeed, x is less than or equal to 10, meaning that 10 is more than or equal to x.
You could also write it this way:
6 < x
That’s because x is more than 6, meaning that 6 is less than x.
Does that make sense? Great! Let’s now move on to how to write an inequality from a word problem.
So as we mentioned before, a word problem presents you with all the information that you need (values), as well as an unknown (variable), and asks you to use the information you have to figure out this unknown.
Inequality equations are one way to solve a problem. Let’s use a slightly modified version of the earlier word problem as an example.
Sally had three pens at the beginning of the school day, but some of her friends gifted her more throughout the day. Despite that, she still didn’t end up with as many as Harry though, who now has a whopping 11 pens in his collection.
There are some simple steps you can follow to translate a word problem into an equation (and, in some cases, solve it). Here they are:
How was that? Is everything making sense, so far?
How about doing it again, using a more complex example?
Imagine that the school teacher has 400 pens at the beginning of the class year. Each month, she gives each student in her class 1 pen. There are 15 students in the class. She must keep at least 100 pens for the end-of-year exam.
How many months can she keep on giving the students pens?
To resolve this, let’s follow the steps.
Now let’s write the equation:
400 - 15m ≥ 100
Let us explain this further:
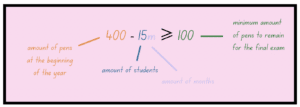
This was an example of a more complex inequality. As you can see, this one contains a subtraction sign and requires some thought.
So now that you know how to write an inequality from number lines or word problems, how about if you wanted to do the exact opposite? By this we mean, what if you wanted to write a number line based on an inequality equation, or to write a word problem based on an inequality equation?
We’re going to show you how to do exactly that.
Let’s use the following inequality as an example:
x < 100
Notice that the value ‘100’ is not included in the solution, since ‘x’ is less than 100, and not ‘less than or equal to’. For this reason, the circle above the number 100 is hollow, as opposed to being filled in.
If the inequality was x ≤ 100, the equation would look like this:

The red circle on top of the number ‘100’ is filled in, because the equation reads ‘less or equal to’.
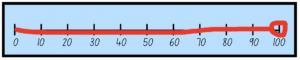
If the equation was x > 100, the equation would read:
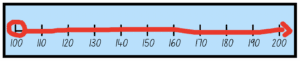
Notice the arrow at the end of the line, to represent infinity, since the equation isn’t specific about the largest number it could be. It only says that it is larger than 100.
To write a word problem from the inequality x > 100 would be pretty straightforward, as this is a simple equation. You just have to get creative!
Come up with a scenario that you can insert a number of items, money, people, or objects into.
Let’s create an imaginary town named Inequiville, and let’s say that last year it had 100 buildings. We know that a planning company came in and built more buildings this year. We just aren’t sure how many.
What do we know? We know there are more than 100. So there you have it. The word problem would sound something like this:
Inequiville had 100 buildings in it last year, but this year a team of builders came in and built more. How many buildings does Inequiville have now?
The answer, as you already know, would be:
x > 100
Once you have written your inequality, the fun doesn’t stop there. If you so choose, you could now go about solving it.
Before you do that, there are a few rules that are handy to know.
If a > b then a + c > b + c
In other words, adding the same number to each side of the equation does not affect the values, nor does it change the direction of the inequality symbol.
If a > b then a - c > b - c
In the same way as above, subtracting the same number to each side neither affects the values nor does it change the direction of the inequality symbol.
If a > b then a * c > b * c
Multiplying each side of the equation by the same positive number is all good in the hood.
If a > b and c is a negative number, then a * -c < b * -c
Multiplying each side of the equation by the same negative number reverses the direction of the symbol.
If a > b then a/c > b/c
Dividing each side of the equation by the same positive number doesn’t change anything.
If a > b and c is a negative number then a/-c < b/-c
Dividing each side of the equation by the same negative number reverses the direction of the symbol.
So, using these rules, let’s see if we can solve earlier’s inequality word problem:
Imagine that the school teacher has 400 pens at the beginning of the class year. Each month, she gives each student in her class 1 pen. There are 15 students in the class. She must keep at least 100 pens for the end-of-year exam.
How many months can she keep on giving the students pens?
As a reminder, the inequality equation we ended up with was this:
400 - 15m ≥ 100
Let’s start by subtracting 400 from both sides.
400 - 400 - 15m ≥ 100 - 400
This leaves us with:
- 15m ≥ -300
Let’s now divide each number by -15.
-15m/-15 ≥ -300/-15
Remember that dividing each side with a negative number reverses the direction of the symbol.
m ≤ 20
So the answer is, that the teacher can give her students a pen per month for 20 months, or less.
Let’s double-check this answer by replacing the variable m with its value 20 in the equation:
400 - 15(20) ≥ 100
400 - 300 ≥ 100
100 ≥ 100
Hurrah! The answer is correct.
As you can see, it works!
That wasn’t so hard, was it? For every complex mathematical concept, there’s always a simple explanation. We believe breaking it down step-by-step always does the trick.
So by now, hopefully, you have a good understanding of what an inequality is, and how to write one from a word problem or a number line. You also know how to do the opposite, and you can resolve an inequality problem, too.
Well done!
We encourage you to share this article on Twitter and Facebook. Just click those two links - you'll see why.
It's important to share the news to spread the truth. Most people won't.
